Welcome to the realm of central angles and arc measures, where we embark on a journey to unravel the intricacies of circular geometry. This comprehensive guide, the ‘central angles and arc measures notes answer key’, serves as your ultimate resource, providing a thorough understanding of these fundamental concepts and their applications.
As we delve into the depths of this topic, we will explore the concept of central angles, their relationship with inscribed angles, and the measurement of arcs using degrees and radians. Moreover, we will establish the direct relationship between central angles and their intercepted arcs, equipping you with the tools to solve practical problems involving these concepts.
Central Angles and Arc Measures: Central Angles And Arc Measures Notes Answer Key
Central angles and arc measures are fundamental concepts in geometry that describe the relationship between angles and arcs on a circle. These concepts have various applications in fields such as engineering, navigation, and astronomy.
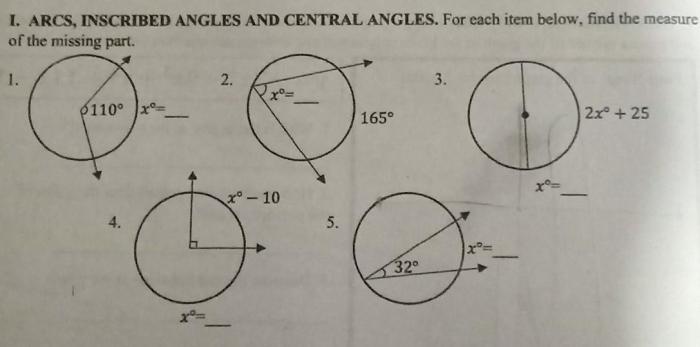
Central Angles
A central angle is an angle formed by two radii of a circle that intersect at the center. The measure of a central angle is the amount of rotation (in degrees or radians) required to move one radius to the other.
- Central angles can range from 0° to 360° (or 0 to 2π radians).
- The sum of the measures of the two central angles that form a straight line is 180° (or π radians).
- Central angles are closely related to inscribed angles, which are angles formed by two chords that intersect inside a circle.
Arc Measures, Central angles and arc measures notes answer key
An arc is a portion of a circle’s circumference. The measure of an arc is the length of the arc expressed in degrees or radians.
- Arc measures can range from 0° to 360° (or 0 to 2π radians).
- The measure of an arc is proportional to the measure of its central angle.
- Degrees and radians are the most common units used to measure arcs.
Relationships between Central Angles and Arc Measures
There is a direct relationship between the measure of a central angle and the measure of its intercepted arc. The formula that expresses this relationship is:
arc measure = (central angle measure / 360°) × 2πr
where r is the radius of the circle.
Applications of Central Angles and Arc Measures
Central angles and arc measures have numerous applications in real-world scenarios, including:
- Navigation: Determining the position of a ship or aircraft using celestial bodies.
- Engineering: Designing gears, pulleys, and other mechanical components.
- Geometry: Solving problems involving circles, angles, and arcs.
Table of Central Angle and Arc Measure Relationships
| Central Angle Measure | Arc Measure | Formula |
|---|---|---|
| α | s | s = (α / 360°) × 2πr |
| α (in radians) | s (in radians) | s = α × r |
Example Problems
- Find the measure of a central angle that intercepts an arc of 60° on a circle with a radius of 10 cm.
- Determine the length of an arc on a circle with a radius of 5 cm if the measure of the central angle that intercepts the arc is 120°.
Frequently Asked Questions
What is a central angle?
A central angle is an angle formed by two radii of a circle that intersect at the center of the circle.
How is arc measure determined?
Arc measure is determined by the ratio of the length of the intercepted arc to the circumference of the circle.
What is the relationship between central angles and arc measures?
The measure of a central angle is directly proportional to the measure of its intercepted arc.