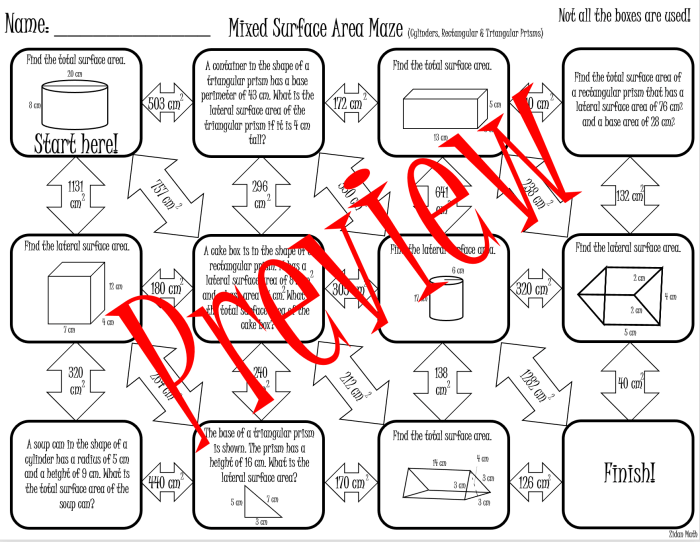
In the realm of geometry, the surface area of prisms and cylinders stands as a captivating concept, inviting us to explore the intricate relationship between shapes and their surface dimensions. With the ‘Surface Area of Prisms and Cylinders Maze’ as our guide, we embark on a captivating journey, where each twist and turn unveils a deeper understanding of this mathematical enigma.
As we navigate this maze, we will unravel the secrets of calculating the surface area of prisms, delving into the nuances of rectangular, triangular, and hexagonal prisms. We will then venture into the cylindrical realm, where we will master the art of determining the lateral and total surface areas of these enigmatic shapes.
Surface Area of Prisms
The surface area of a prism is the total area of all its faces. It can be calculated using the formula: Surface Area = 2(lw + lh + wh)
where l is the length, w is the width, and h is the height of the prism.
Rectangular Prisms
Rectangular prisms have six rectangular faces. The surface area of a rectangular prism can be calculated using the formula:
Surface Area = 2(lw + lh + wh)
Triangular Prisms, Surface area of prisms and cylinders maze
Triangular prisms have two triangular faces and three rectangular faces. The surface area of a triangular prism can be calculated using the formula:
Surface Area = 2(1/2bh + lw + lh)
where b is the base of the triangle.
Hexagonal Prisms
Hexagonal prisms have two hexagonal faces and six rectangular faces. The surface area of a hexagonal prism can be calculated using the formula:
Surface Area = 2(1/2as + lw + lh)
where a is the apothem of the hexagon.
Surface Area of Cylinders
The surface area of a cylinder is the total area of its lateral surface and its two circular faces. The lateral surface area is the area of the curved surface of the cylinder, while the total surface area includes the lateral surface area and the areas of the two circular faces.
Lateral Surface Area
The lateral surface area of a cylinder can be calculated using the formula:
Lateral Surface Area = 2πrh
where r is the radius of the base and h is the height of the cylinder.
Total Surface Area
The total surface area of a cylinder can be calculated using the formula:
Total Surface Area = 2πr(r + h)
Commonly Asked Questions: Surface Area Of Prisms And Cylinders Maze
What is the formula for calculating the surface area of a rectangular prism?
2(lw + lh + wh)
How do I find the total surface area of a cylinder?
2πr(r + h)
What is the relationship between the surface area of a prism and its volume?
The surface area of a prism is directly proportional to its volume.