Embark on an enlightening journey with our Parallel and Transversal Lines Quiz, meticulously crafted to challenge your comprehension of these fundamental geometric concepts. Dive into the captivating world of parallel and transversal lines, where intersecting paths reveal intriguing relationships and angle formations.
Prepare to navigate through a series of thought-provoking questions that will test your grasp of parallel and transversal lines. Each question is carefully designed to assess your understanding of their properties, angle relationships, and practical applications. Get ready to put your knowledge to the test and emerge with a deeper appreciation for these geometric marvels.
Definitions
Parallel lines are straight lines that never intersect, no matter how far they are extended. Transversal lines are lines that intersect two or more other lines at distinct points.
Relationship between Parallel and Transversal Lines
When a transversal line intersects two parallel lines, it creates four angles. These angles are related to each other in specific ways, as described by the following theorems:
- Alternate Interior Angles Theorem:The alternate interior angles formed by a transversal intersecting two parallel lines are congruent.
- Corresponding Angles Theorem:The corresponding angles formed by a transversal intersecting two parallel lines are congruent.
- Same-Side Interior Angles Theorem:The same-side interior angles formed by a transversal intersecting two parallel lines are supplementary.
Properties of Parallel and Transversal Lines
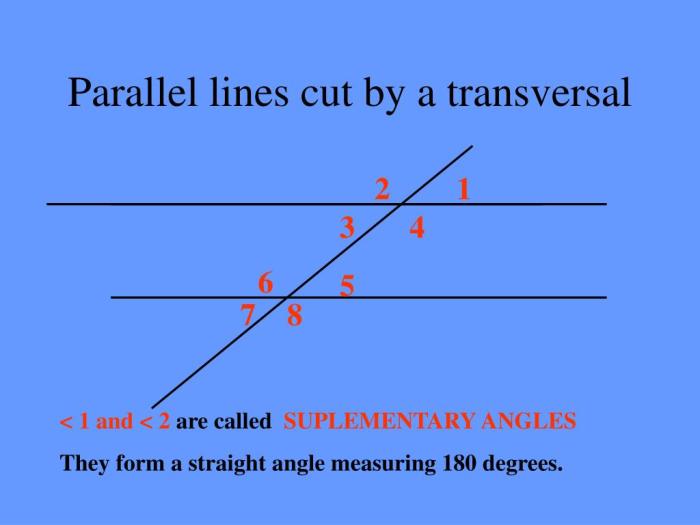
Parallel lines are lines that never intersect. When a transversal intersects two parallel lines, it creates eight angles. The properties of these angles can be used to solve problems involving parallel lines and transversals.
Properties of Parallel Lines Cut by a Transversal
When a transversal intersects two parallel lines, the following properties hold true:
- The alternate interior angles are congruent.
- The alternate exterior angles are congruent.
- The consecutive interior angles are supplementary.
Properties of Transversal Lines that Intersect Parallel Lines
When a transversal intersects two parallel lines, the following properties hold true:
- The transversal is perpendicular to both parallel lines.
- The segments created by the transversal on the parallel lines are congruent.
| Property | Description |
|---|---|
| Alternate interior angles | Congruent |
| Alternate exterior angles | Congruent |
| Consecutive interior angles | Supplementary |
| Transversal perpendicular to parallel lines | True |
| Congruent segments on parallel lines | True |
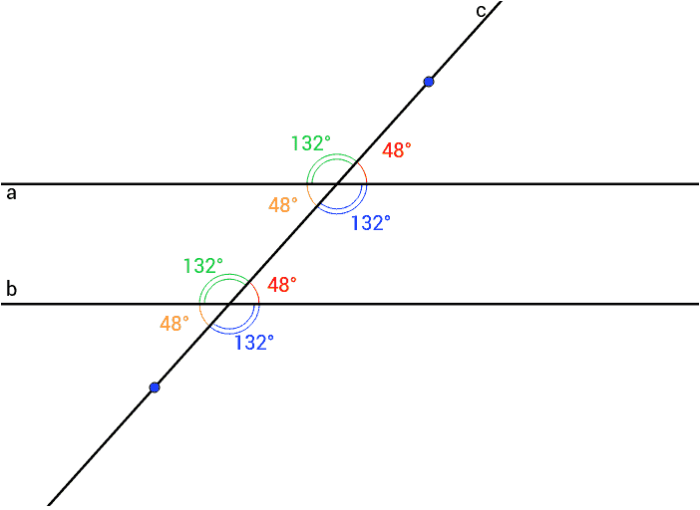
Angle Relationships
When parallel lines are cut by a transversal, several special angle relationships are formed.
Alternate Interior Angles
Alternate interior angles are pairs of non-adjacent angles that lie on opposite sides of the transversal and inside the parallel lines. These angles are congruent, meaning they have the same measure.
Corresponding Angles
Corresponding angles are pairs of angles that lie on the same side of the transversal and outside the parallel lines. These angles are also congruent.

In the diagram above, ∠1 and ∠5 are alternate interior angles, and they are congruent. ∠2 and ∠6 are corresponding angles, and they are also congruent.
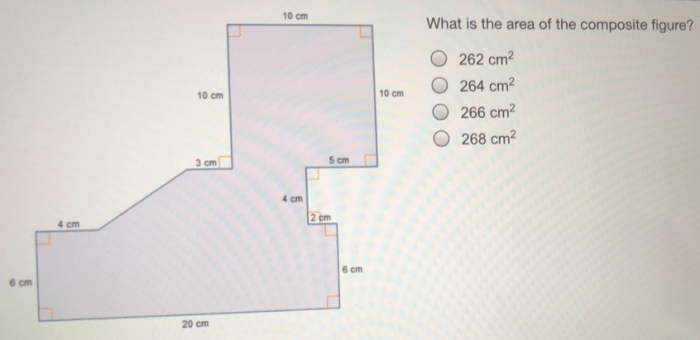
Solving Problems: Parallel And Transversal Lines Quiz
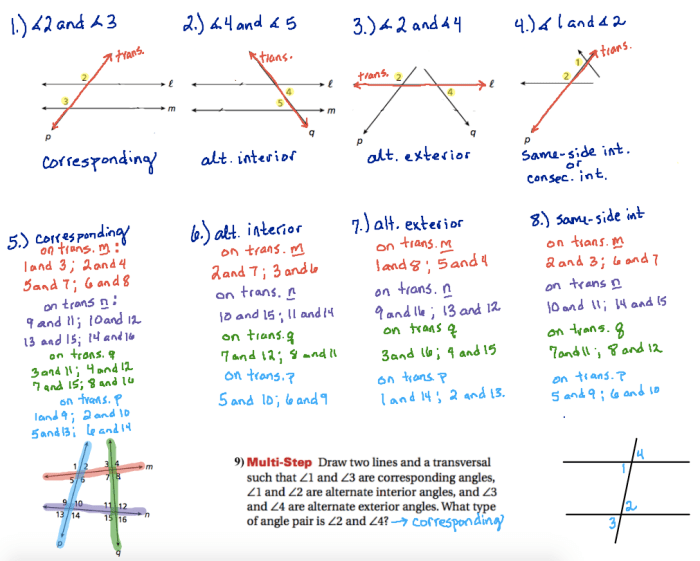
Solving problems involving parallel and transversal lines requires understanding the properties and angle relationships between them. These problems can be solved by applying the properties of parallel lines, such as alternate interior angles and corresponding angles, and by using the relationships between angles formed by a transversal intersecting parallel lines.
Examples of Problems, Parallel and transversal lines quiz
- Find the measure of angle x in the diagram, where line AB is parallel to line CD and transversal line EF intersects both lines.
- Determine if lines AB and CD are parallel if angle 1 is congruent to angle 4 and angle 2 is congruent to angle 3.
- Find the value of x if lines AB and CD are parallel and angle 1 is 50 degrees.
Steps to Solve Problems
- Identify the parallel lines and the transversal line.
- Apply the properties of parallel lines to identify congruent angles or relationships between angles.
- Use the angle relationships to solve for the unknown angle or value.
Practice Exercise
Problem:In the diagram below, line AB is parallel to line CD. Find the measure of angle x.[Image of a diagram with line AB parallel to line CD, transversal line EF intersecting both lines, and angle x marked.]Solution:Identify the parallel lines and the transversal line.
-
2. Apply the alternate interior angles property
angle x is congruent to angle 3.
- Since angle 3 is given as 60 degrees, angle x is also 60 degrees.
Therefore, the measure of angle x is 60 degrees.
Applications
Parallel and transversal lines find practical applications in various fields, including architecture, engineering, and design. Their properties and relationships are utilized to create structures, solve geometric problems, and ensure stability and aesthetic appeal.
Architecture
In architecture, parallel lines are commonly used to create symmetry and balance in building designs. Parallel walls, columns, and windows provide a sense of order and harmony. Transversal lines, on the other hand, are used to create intersections and connect different parts of a structure.
For example, the intersecting lines of a roof truss provide support and stability to the building.
Engineering
In engineering, parallel and transversal lines are used in the design and construction of bridges, roads, and other infrastructure. Parallel beams and girders provide structural support, while transversal beams and trusses distribute loads and ensure stability. The angles formed by intersecting lines are carefully calculated to optimize strength and minimize stress.
Design
In design, parallel and transversal lines are used to create visual interest and balance in artwork, graphic design, and interior decor. Parallel lines can create a sense of rhythm and movement, while transversal lines can create contrast and depth. The use of these lines can enhance the overall aesthetics of a design and guide the viewer’s eye.
Commonly Asked Questions
What is the key characteristic of parallel lines?
Parallel lines never intersect, maintaining a constant distance from each other.
How do you identify transversal lines?
Transversal lines intersect two or more other lines at distinct points.
What is the relationship between alternate interior angles when parallel lines are cut by a transversal?
Alternate interior angles are congruent, meaning they have the same measure.